Tank Rover: Animations
In my robotics post on the remote-controlled tank rover and my demonstration video, I had included some animations illustrating the various major components on the rover. Those graphics are generated programmatically using Mathematica—and in this write-up I'll narrate how it was done. If you're attempting to do similar things, hopefully you'll find this useful.
As with all things Lego we start with a CAD mock-up in Lego Digital Designer (LDD). I'd previously outlined a simple workflow to generate Wavefront Object models from LDD files in my blog post on the six-speed gearbox—in brief one imports the LDD file in an open-source software LeoCAD, preserve the portions of the model one desires, and export as either 3DS or Wavefront Object files. This exported model can then be manipulated in Mathematica for rendering.
The difference between 3DS and Wavefront Object models is that the former encodes material information in addition to geometry, whereas the latter encodes only the model geometry. Upon importing into Mathematica, a 3DS model would be parsed into a GraphicsComplex object with all colour information preserved, whereas a Wavefront Object model would be parsed into a MeshRegion, with no styling whatsoever.
It seems as though using 3DS is less restrictive and hence a superior approach, but it turns out that the polygon-by-polygon colour styling puts a tremendous overhead on rendering, so much so that working with large models is incredibly slow, and oftentimes outright unresponsive. In addition, manipulating a MeshRegion—for instance translation, rotation, and scaling—is much easier than manipulating a GraphicsComplex object. Hence it is simply not true that one is inferior to the other.
It is better to examine the various animations separately, for different approaches are involved. Let us start with the ones shown on my robotics page, and in the middle of the video—the rotating schematics with component-wise colour shading. We'll examine the Lego variant animation first.
Schematic Animation (Lego)

These animations are very much like the still illustrations I'd created for my six-speed gearbox, with a rotation thrown into the mix. Unsurprisingly the starting steps are similar to those for the gearbox. We import Wavefront Object models, one for the complete rover, and one for each desired coloured component. The idea is that we'll overlap them to create the final renderings.

Before we proceed further, we might wish to introduce our own colour palette, so that our renderings would suit the style of whatever medium we intend to include these animations in. For my purposes I'd gone with a chalk colour theme, so that the colours are softer to the eyes. We can easily define custom colours using RGB values, or alternatively hexadecimal, using the RGBColour function.

To check that our idea of overlapping the various models does indeed work, we can write a rudimentary Show block as a proof-of-concept. We can use the MeshCellStyle option of MeshRegion to control the colour of each of our models—we set the entire tank to be translucent, and we style each of our components a distinct colour. We select the {2, All} elements of the geometry to style, which corresponds to all polygons in the mesh; using {1, All} instead would select all lines, and {0, All} would select all vertices. It is therefore possible to apply styling much more complex than what we're doing here.

Now the idea is that we render our animations frame-by-frame, with the model rotated a little from one frame to the next, so that when put together as a video the model appears to spin about its center. A reality check—rotating a mesh is perfectly doable, for instance by multiplying each vertex position by a rotation matrix and then reconstructing the polygons. And in fact Mathematica already has built-in functions to apply geometric transformations to MeshRegions. So we're not too concerned about that. This method, however, works only when the model is centered—else the model would translate as perceived from our fixed viewpoint, and the animation would not look good.
And therefore we have to make sure that our model is as centered as possible, with respect to the origin. In general models built in LDD or LeoCAD would not be centered. We can fix this by averaging all vertex positions to find the mean, and then translating the entire model to compensate. We have to compensate by this same amount for all other models as well. We can use the TransformedRegion function in Mathematica to build what are essentially new MeshRegions, derived from our imported models through a TranslationTransform.

Now we deal with the rotation. Analogously we use TransformedRegion to build the rotated models, this time with RotationTransform instead of TranslationTransform. The first argument passed into RotationTransform is the angle to rotate by, and the second, the axis of the rotation. For our purposes the vector would be a vertical one—in our Cartesian coordinate system, {0, 0, 1}. An optional third argument specifies a reference point about which the rotation is performed; since we have set everything up to rotate about the origin, we need not specify this argument.
We can indeed test that this works by using either a Manipulate block, or an Animate block. We set the resolution of rotation angle to be quite coarse, so that the computer doesn't give up and die; and by dragging the slider we can see that the model does indeed rotate.

So we have figured out the necessary manipulations for the model itself, which wasn't too hard. Now we need to figure out how to add the labels. Again, a reality check—Mathematica does have a function appropriately named Text, which provides a graphics primitive for either 2D or 3D use. We also have a function named Line to conveniently draw lines, or in fact a series of lines, in 3D space. And lastly the positions and directions of both Text and Line can be freely specified, so they fit our needs just fine.
Our idea is that, for the sake of standardization, all labeling lines should ideally originate from the origin—that is, if they are all extended backwards, they should all meet neatly at a single point, at the origin. This way our labelled model would most likely look neat. But things seldom work out this simply, and the problem is that the components we wish to label have very different positions, and constraining all labeling lines to intersect at the origin would mean that some labels are too high, or too low, or that they visually obstruct one another. And so we wish to introduce some form of tuneable correction vector, to modify this point of origin for individual lines. This vector should, by its nature, not be very large in magnitude.

And so we can draw the geometry for labeling as shown above. There's a slight inaccuracy in the diagram—the coordinate system drawn is left-handed when it should be right-handed—but never mind that. We have an offset vector defining an effective origin, and an anchor point, which is the position of the component we wish to label. These two points determine the direction of the labeling line. At some specified distance from the anchor point we have the label itself. We also introduce a start padding and an end padding.
We can define a function, which we named LabelF, to render a label in accordance to the scheme we devised. Because Text and Line returns graphics primitives, not MeshRegions, we use Rotate to transform and place them. Notice also that we are able to customize the font for the label—this is manually tweaked to match the size of the model.

And now we can define another function, which I had named GraphicsF, to generate a complete frame at some certain rotation angle. We'll call this function repeatedly in a loop sometime later, in order to generate the hundreds of frames that we need. In this function we have a huge Show block encapsulating the various models and labels that we wish to include. The rendering of the models is accomplished through the TransformedRegion approach we'd established, and indeed tested, earlier on; and the rendering of the labels is accomplished through our LabelF function.

Notice that we have set a customized PlotRange, which we manually tweak to ensure that all parts of our model and labels can be seen throughout the rotation. We have also measured the positions of the components we wish to label (LeoCAD does show the coordinates of selections).
We desire that only the model and labels be shown, without any bounding boxes or axes, so rightfully the Boxed option should be set to false; but a complication is that Mathematica tends to ignore our customized PlotRange if no bounding boxes is drawn. We therefore employ a workaround, by setting Boxed to true, and at the same time set the box opacity to an extremely small number, so that it is effectively invisible.
With all this done, we now need only call GraphicsF iteratively. Here we need to be aware of how massive a computational job this would be. Generating a 30 frames per second animation that lasts half a minute—which is more or less the kind of rotational speed we desire—would require some 900 frames, and if each frame takes 3 minutes to generate, we're looking at 45 hours of work. The only way this can be made more reasonable is to exploit parallelism. Supposing an ideal case of perfect scalability, spreading the work over four threads would bring the time down to about 11 hours, which is quite manageable.
The good news is that processor-intensive jobs generally scale pretty well in Mathematica, so we're in good hands. The bad news is that parallelizing the code does make things a little complicated.
The first complication is that 3D graphics manipulation inevitably takes humongous amounts of memory—about 2 GB per running kernel, and up to 3 GB peak—and running numerous kernels in parallel exacerbates this issue. Taking into account the memory overhead of the master kernel, the fundamental limiting factor we are likely to face is the available RAM, instead of processor power. With 8 GB of memory two slave kernels is reasonable; with 16 GB, four slaves. Anything lower than 8 GB and sequential evaluation might be preferable, and anything greater than 16 GB would likely allow the processor to reach maximum utilization, free of memory bottlenecks. The message is that the questions of how many kernels to run, and whether or not parallelism would be beneficial in the first place, is dependent on the specific machine used.
Another thing we have to note is that due to the memory intensiveness of this job, things might fail, and they might fail due to a variety of reasons and internal cock-ups we cannot possibly eliminate. So we must have a mechanism in place to catch these failures. We employ two approaches, each to manage failures at different levels. At the thread level, we can put a time constraint on the rendering of each frame—so that if things get stuck, the rendering would be timely terminated, and the kernel can continue with other jobs.
At a higher level, we put a time constraint on the entire loop, and we restart all kernels when this constraint expires, so that memory leaks, if any, and runaway kernels are eliminated, and the rendering process can resume with fresh resources. To get this to work we need to have a persistent way of checking for frames that had already been rendered in previous loops, and we do indeed have an easy solution—simply check the list of files in the export directory.
With all these ideas in mind, we can write the pseudo-code as follows.

And the actual Mathematica code goes something like this:

Note the use of SetSharedVariable—it tells Mathematica that the same counter variable instance is to be shared by all kernels. Else each kernels would have its own instance of counter, and our progress indicator would not work. Also note that we have set the size of the rendered frames to be 2560 pixels in width; this is a compromise between fidelity and speed, and can be set higher or lower as one wishes. The rotation angle resolution is set such that the full 360-degree animation would cover 32 seconds at 30 frames per second.
All that is left is to run the chunk of code, and wait—and wait for pretty damn long. It took slightly more than 12 hours on my machine.
Following this, the exported frames are imported into a video editing software as an image sequence. I used Vegas Pro, but almost any modern software would do. Crop as desired, and render the animation out as a video.
Making the animation into a GIF is a little trickier, and I'd already written about this in a previous blog post. In essence one can use the free software GIMP to import all the frames as layers of a single image, crop and scale as desired, and then convert the image to indexed mode. The greater the number of indexed colours used, the better the colour fidelity of the final GIF, but the larger the file size; so if file size is a concern, one might have to limit the image size and the number of indexed colours. The image can then be exported as a GIF, with an appropriate frame rate.
And that's it for the Lego variant animation. The Arduino variant is a little more difficult, as we'll see, because we have to scale, rotate and position the non-Lego component models suitably.
Schematic Animation (Arduino Variant)
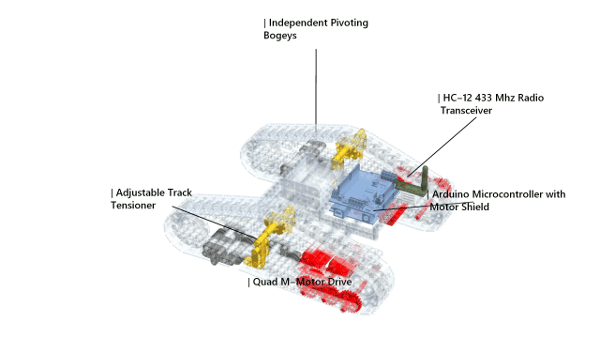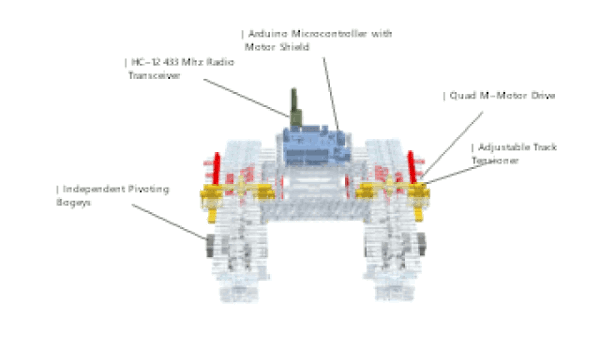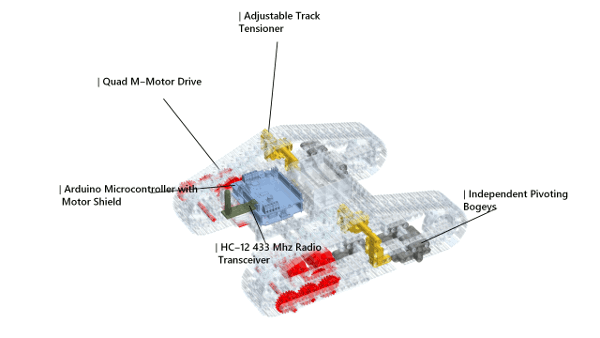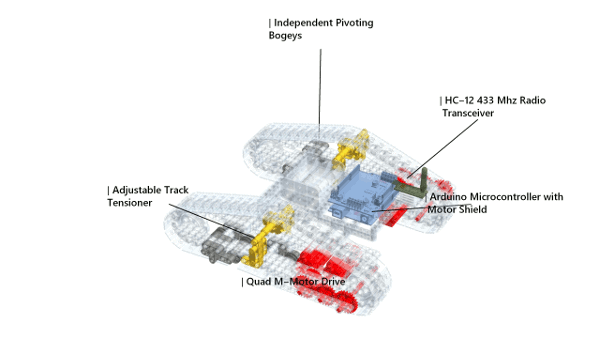
We can use the same framework to produce the animation for the Arduino variant, but because we are combining models made in LeoCAD and other CAD software—SolidWorks in my case—we would have to be cautious when positioning them. The creation of models in SolidWorks or any other CAD software is out of the scope of this article, and so I shall not discuss it; but it might be helpful to note that even without CAD knowledge, one can easily obtain and manipulate models, by downloading them from sites such that GrabCAD, or Blend Swap, or SketchUp's 3D Warehouse.
In general, the coordinate system in which the various non-Lego components are created in can be different from that of LeoCAD, and the orientation and scale of the various models would almost always be different. And so it is necessary for us to rotate and scale them all to the same standard.
In our case it would make sense to take the Lego models as reference. I'll present the code used for importing the Arduino model first, and then explain the various steps involved, since this might be easier.

The first and second lines are standard. The third and fourth lines—those involving RotationTransform—are there to correct the orientation of the Arduino model. The model seems to be upside-down, and so a 180-degree flip about the y-axis is done to correct it; a similar flip around the x-axis would, of course, also work. Following this flip, the Arduino is facing the wrong direction—the power port needs to be on the left side of the tank rover—and so a rotation about the vertical is done.
And then we scale the Arduino to be of the right size, relative to the Lego models. We use RegionBounds to find out the width of the model. Further, we know that the Arduino in real-life measures about 7.5 centimeters wide, and also that one distance unit in LeoCAD corresponds to 4 millimeters, half the standard pitch of Lego. This allows us to determine the necessary scaling ratio for the Arduino model, which is plugged into ScalingTransform.
And lastly, by scrutinizing the rover inside LeoCAD, we determine that the appropriate position for the Arduino is approximately {1053, 123, -203} in the local frame. But we must remember that we had shifted this frame by some distance in order to bring the tank rover to the origin, and this is why we have {1053, 123, -203}-mean.
The same process is repeated for all the other electronic components—the motor shield, the HC-12 module, the antenna, the battery holder. The process, of course, necessitates frequent checks to make sure everything lines up.

And of course, now we just need to modify our GraphicsF function, and we can call the same parallelized rendering algorithm to crunch through the frames.

Schematic Animation (Opening Sequence)
And finally we'll discuss how the opening sequence of my demonstration video was made. The opening sequence goes something like this, if you have not yet watched the video. It's the first eleven seconds of the video, approximately.
It's pretty easy to dissect. It's essentially a fading transition between three clips—the first being a coloured tank rover, the second, a translucent one with colours removed, and the third, the Lego variant schematic animation we'd examined in detail earlier on.
Generating the translucent clip is trivial; it simply involves removing all models save the tank model, and removing all LabelF calls in GraphicsF. The parallelized algorithm can then be used without modification to generate the frames. And then one imports everything into a video editor and renders it into video format; or into GIMP for a GIF.


The full-colour clip is more tricky. One can, of course, simply export the tank rover model out of LeoCAD as a 3DS file, which preserves colour information. The file can then be imported into Mathematica, which automatically parses it into a Graphics3D object.

To obtain the geometric center of the model now becomes non-trivial; we have to dig deep into the structure of Graphics3D and access the vertices manually. Translating and rotating the model similarly becomes non-trivial; we have to manually dig out the vertices, modify them, and then reconstruct the Graphics3D layer-by-layer.
Something that's not apparent in the documentation of Mathematica—one can use the Part function to break virtually any object into its constituents. Accessing the zeroth element of any object would give the Head of that object, equivalent to calling Head explicitly; in our case, selecting the zeroth element of our imported model would return Graphics3D. When we access the first element of the model, however, something interest crops up.

We observe that buried somewhere in that first element is a GraphicsComplex object, and inside it, there are two lists—the first being a vertex list, and the second being a list of alternating colours and polygons, which encodes the colour information of the model. And not only is there a single GraphicsComplex object—there is in fact 442 of them! Incidentally there are 442 parts in our Lego model, and this implies that each Lego part is in fact encoded in a distinct GraphicsComplex object. This hierarchical structure must have been preserved by LeoCAD when exporting into the 3DS format, and it is again preserved upon importing into Mathematica. How fascinating!
In any case we see that the polygon specifications pass only vertex indices as arguments, which means we are free to modify the positions of the vertices without any need to touch the second list at all, so long as we preserve the order of the vertices. This would simplify our work later, when transforming the model. Now we concern ourselves with the evaluation of the geometric center of the model, which can be accomplished as follows.

And now, we define the GraphicsF function. We use TranslationTransform to construct a transformation function, which we apply to the vertex lists of all GraphicsComplex objects in order to bring the model to the origin. A RotationTransform is applied on top of that, to accomplish the rotation for the animation. And then we reconstruct everything else around these transformed vertex lists—we add in the colour specifications, the lighting, and the EdgeForm.

And it indeed does work.

The only problem is, doing things this way takes incredibly long—each frame takes more than twice as long to generate, as opposed to the Wavefront Object approach. Memory requirements are similarly larger. And so, while this is indeed a way of generating the animations, it is one of limited viability.
We hence fall back to the Wavefront Object method. But now that the colour information is removed, we'll have to add it back using MeshCellStyle, as we had done for labeling purposes earlier; and to do so, we'll have to create separate models, each containing the parts of a different colour. In other words, all black-coloured parts are to be in one model, all yellow-coloured parts are to be in another, and so on. It is a tedious process to create these models in LeoCAD, but the speed-up in computation time is dramatic.


We can reference the Lego colour palette generously compiled here, in order to style the various MeshRegions appropriately. We also set the opacity to 0.8, so that the shading isn't too harsh, and we can see slightly through to obstructed parts.

And then we define our GraphicsF function.

And then we're done. Simply use the parallelized algorithm to generate the frames, and do some video editing.

Phew. This was an awfully long post to write. I really hope you have found a thing or two in this post interesting. And yes, there's even more Mathematica behind-the-scenes, involved in the production of this blog post itself—in the cropping of screenshots, especially. But that is for another time. Until then, goodbye!